Terug naar Opgaven Som- en verschilformules
Opgave 1
Toon aan dat geldt:
![]()
Uitwerking
In het rechter lid substitueren we:
![]()
en krijgen:
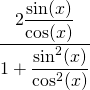
We vermenigvuldigen teller en noemer met ![]() :
:
![]()
Terug naar Opgaven Som- en verschilformules
Terug naar Opgaven Som- en verschilformules
Toon aan dat geldt:
![]()
In het rechter lid substitueren we:
![]()
en krijgen:
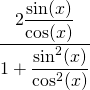
We vermenigvuldigen teller en noemer met ![]() :
:
![]()
Terug naar Opgaven Som- en verschilformules