Optimaliseren f(x)

Samenvatting en voorbeelden

$f'(a)$ is de afgeleide van een functie $f(x)$ in een punt $(a,f(a))$ en is de richtingscoëfficiënt van de raaklijn in dat punt.

Wanneer $f'(a)=0$ betekent dit dat de raaklijn in $(a, f(a))$ een richtingscoëfficiënt $0$ heeft en dus evenwijdig aan de $X$ -as loopt. Voor een dergelijk punt geldt een van de volgende drie mogelijkheden:

het punt is een (lokaal) maximum;
het punt is een (lokaal) minimum;
het punt is een horizontaal buigpunt (een voorbeeld hiervan is de grafiek van $y=x^3$ ).

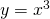Wanneer we willen weten in welke punten een functie $f(x)$ een lokaal maximum, minimum of een horizontaal buigpunt heeft, dan berekenen we de afgeleide $f'(x)$ , stellen die gelijk aan $0$ en lossen de resulterende vergelijking op. Immers, we vinden op deze manier de waarden van $x$ waarvoor de afgeleide gelijk aan $0$ is.

Voorbeeld 1

Bepaal het minimum van de parabool:

$y=2x^2-8x-4$

We weten al dat de parabool een dalparabool is (de coëfficiënt van het kwadraat is $2$ en dus groter dan $0$ ) en dus een minimum heeft.

We differentiëren de functie en krijgen:

$y'=4x-8=0$

en dus:

$x=2$

De parabool heeft dus een minimum in het punt $(2,-12)$ .

Voorbeeld 2

Bij tweedegraads functies (de grafieken van dergelijke functies zijn parabolen):

$y=ax^2+bx+x, (a\neq0)$

hebben we al met behulp van de abc-formule kunnen berekenen dat de top ligt op de symmetrie-as en dat dus geldt:

$x_{top}=-\displaystyle\frac{b}{2a}$

We kunnen dit nu ook met behulp van differentiëren berekenen. De afgeleide van bovenstaande functie is:

$y'=2ax+b$

De afgeleide is gelijk aan $0$ (in de top) wanneer:

$x=-\displaystyle\frac{b}{2a}$

welke de $x$ -coördinaat van de top is.

Door van een functie de afgeleide gelijk aan $0$ te stellen, vinden we de kandidaten voor een mogelijk maximum, minimum of horizontaal buigpunt, maar we weten dan nog niet met welk van de drie we te maken hebben. Daarvoor is nader onderzoek nodig. Er zijn hiervoor twee verschillende methoden.

Methode 1: tekenoverzicht van de eerste afgeleide

In een maximum in een punt met $x=a$ is de afgeleide $0$ . Links van het maximum is de functie stijgend en dus geldt $f'(x)>0$ voor $x<a$ . Rechts van het maximum is de functie dalend en dus is $f'(x)<0$ voor $x>a$ . Dus er geldt voor $f'(x)$ rond het maximum in $x=a$ het volgende tekenoverzicht:

maximum : + 0 -.

Op dezelfde wijze geldt dat voor $f'(x)$ rond een minimum in een punt met $x=a$ het volgende tekenoverzicht geldt:

minimum : - 0 +.

Voor een horizontaal buigpunt vinden we het volgende tekenoverzicht:

horizontaal buigpunt : + 0 + of - 0 -.

Methode 2: onderzoek van de 2e afgeleide

Wanneer $x=a$ een van de oplossingen van de vergelijking $f'(x)=0$ is en dus een kandidaat voor een maximum, minimum of een horizontaal buigpunt, dan geldt het volgende. Als:

$f''(a) > 0$ , dan is er in $x=a$ een minimum;

$f''(a) < 0$ , dan is er in $x=a$ een maximum;

$f''(a) = 0$ , dan is er in $x=a$ een buigpunt.

Voorbeeld 3

Ga na of de functie:

$y=\displaystyle\frac{1}{3}x^3-x+1$

een maximum en/of minimum heeft.

De afgeleide is:

$y'=x^2-1$

De afgeleide is $0$ als:

$x^2-1=0$

dus als:

$x=1$ of $x=-1$

De overeenkomstige punten op de grafiek zijn respectievelijk:

$(1,\displaystyle\frac{1}{3})$ of $(-1,-\displaystyle\frac{5}{3})$

We gaan nu de beide methoden na.

Methode 1

Voor $x=-1$ vinden we het volgende tekenoverzicht van $f'x)$ :

+ 0 - en dus is er sprake van een maximum.

Voor $x=1$ vinden we het volgende tekenoverzicht van $f'(x)$ :

- 0 + en dus is er sprake van een minimum.

Methode 2

We moeten eerst de tweede afgeleide bepalen:

$y''=2x$

Er geldt:

$y''(-1)=-2<0$ en dus is heeft de functie voor $x=-1$ een maximum, en

$y''(1)=2>0$ en dus heeft de functie voor $x=1$ een maximum.

Het zal niet verbazen dat beide methodes tot dezelfde uitkomst leiden.

Voorbeeld 4

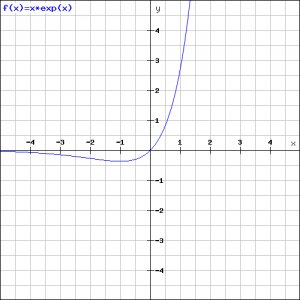
Ga na of de functie:

$y=xe^x$

een lokaal maximum of minimum heeft.

De afgeleide van de functie is, met gebruikmaking van de productregel:

$y'=1.e^x+xe^x=(x+1)e^x$

De afgeleide is 0 wanneer x=-1 en het punt $(-1, e^{-1})$ is daarmee een kandidaat voor een maximum of minimum. Nader onderzoek moet uitwijzen welke van de twee het is. Het is zelfs mogelijk dat het een buigpunt is.
We kunnen beide methoden gebruiken, maar de tweede methode is bewerkelijker omdat voor het berekenen van de tweede afgeleide opnieuw de productregel moet worden gebruikt. We kiezen daarom voor methode 1 en hoeven alleen maar naar het teken van $x+1$ te kijken omdat de exponentiële functie $e^x$ altijd positief is.