Samenvatting en voorbeelden
De volgende formule is een voorbeeld van een exponentiële functie:
![]()
waarbij moet gelden ![]() . De naam exponentiële functie wordt gebruikt wanneer de onafhankelijke variabele
. De naam exponentiële functie wordt gebruikt wanneer de onafhankelijke variabele ![]() voorkomt in de exponent. De bovenstaande functie is steeds positief. Immers, de macht van een positief getal is altijd positief.
voorkomt in de exponent. De bovenstaande functie is steeds positief. Immers, de macht van een positief getal is altijd positief.
Natuurlijk kan een dergelijke functie nog worden uitgebreid, bijvoorbeeld:
![]()
![]() ,
, ![]() ,
, ![]() ,
, ![]() en
en ![]() zijn constanten en worden ook wel parameters genoemd.
zijn constanten en worden ook wel parameters genoemd.
We zullen de grafieken tekenen van twee exponentiële functies.
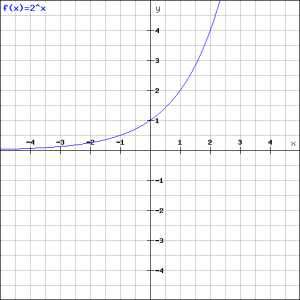
De linker grafiek behoort bij de functie:
![]()
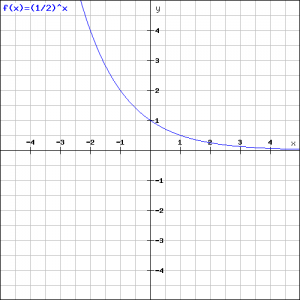
De rechter grafiek hoort bij de functie:
![]()
Beide grafieken zijn elkaars spiegelbeeld, ze spiegelen in de ![]() -as. We kunnen dat ook algebraïsch gemakkelijk inzien:
-as. We kunnen dat ook algebraïsch gemakkelijk inzien:
![]()
en dat is het spiegelbeeld in de ![]() -as van de functie:
-as van de functie:
![]()
We zullen enkele functies van het type:
![]()
in een grafiek samenbrengen, namelijk:
![]()
![]()
![]()
Zie de figuur.
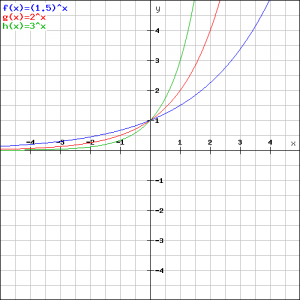
Het eerste dat opvalt is dat alle drie grafieken door het punt ![]() gaan. Dat is niet zo verwonderlijk, immers voor
gaan. Dat is niet zo verwonderlijk, immers voor ![]() geldt:
geldt:
![]()
voor elke ![]() .
.
Verder is het gemakkelijk te verklaren dat de snelst stijgende grafiek (groen) hoort bij de functie:
![]()
en de minst snel stijgende grafiek (blauw) bij de functie:
![]()
Verder zien we dat alle drie grafieken naar ![]() gaan wanneer we
gaan wanneer we ![]() steeds negatiever nemen. Met andere woorden, als:
steeds negatiever nemen. Met andere woorden, als:
![]() dan
dan ![]()
De grafieken zullen in theorie de ![]() -as niet bereiken, maar komen er wel steeds dichterbij. Een dergelijke lijn, in dit geval de
-as niet bereiken, maar komen er wel steeds dichterbij. Een dergelijke lijn, in dit geval de ![]() -as, noemen we een asymptoot.
-as, noemen we een asymptoot.
Nu zullen we kijken naar een wat ingewikkelder exponentiële functie:
![]()
In de figuur is de grafiek van deze functie getekend.
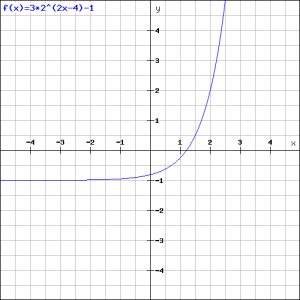
Als ![]() krijgen we:
krijgen we:
![]()
en dat lijkt in de figuur wel te kloppen.
Willen we weten waar deze functie de ![]() -as snijdt, dan moeten we
-as snijdt, dan moeten we ![]() kiezen. We krijgen dan de volgende exponentiële vergelijking (zie ook het onderwerp Exponentiële vergelijkingen):
kiezen. We krijgen dan de volgende exponentiële vergelijking (zie ook het onderwerp Exponentiële vergelijkingen):
![]()
![]()
Wanneer we van het linker en rechter lid de logaritme nemen (zie ook het onderwerp Logaritmische functies en grafieken), krijgen we:
![]()
![]()
![]()
en dat lijkt redelijk overeen te komen met de figuur. (Vaak is het niet nodig een precies getal te berekenen en kunnen we volstaan met een antwoord waarin nog logaritmen voorkomen).
Tenslotte zien we dat als ![]() steeds negatiever wordt, dus als
steeds negatiever wordt, dus als ![]() de eerste term van de functie naar
de eerste term van de functie naar ![]() gaat en dus de grafiek nadert naar de waarde
gaat en dus de grafiek nadert naar de waarde ![]() . Ook dat kunnen we goed in de figuur waarnemen.
. Ook dat kunnen we goed in de figuur waarnemen.
Voorbeeld 1
Teken de grafiek van:
![]()
We kunnen de grafische rekenmachine gebruiken, maar de praktijk leert dat het begrip van de stof hierdoor eerder af- dan toeneemt. Daarom proberen we de grafiek met de hand te tekenen.
We proberen een aantal punten te vinden om op die wijze de grafiek te kunnen schetsen.
Voor ![]() krijgen we achtereenvolgens:
krijgen we achtereenvolgens:
![]()
![]()
![]()
![]()
![]()
en dus kunnen we de grafiek tekenen:
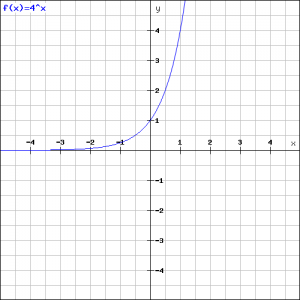
Voorbeeld 2
Teken de grafiek van:
![]()
We beschouwen eerst de functie:
![]()
dan kunnen we daarna de oorspronkelijke functie tekenen door bij het resultaat steeds 1 op te tellen.
We proberen een aantal punten te vinden om op die wijze de grafiek te kunnen schetsen.
Voor ![]() krijgen we achtereenvolgens:
krijgen we achtereenvolgens:
![]()
![]()
![]()
![]()
![]()
Zie de figuur.
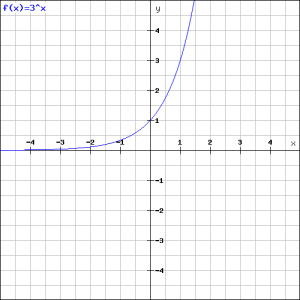
Het uiteindelijke resultaat krijgen we door bij deze grafiek 1 op te tellen:
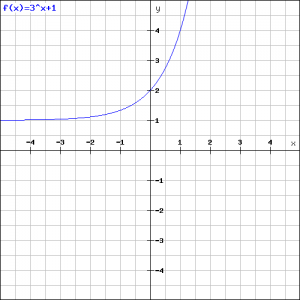
Voorbeeld 3
Teken de grafieken van:
![]()
![]()
en bereken hun snijpunt.
We weten globaal hoe de grafieken moeten lopen, zie boven. In de onderstaande figuur zijn ze precies getekend. Ga na welke grafiek hoort bij welke functie.
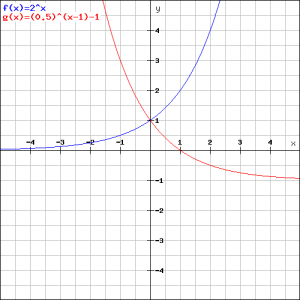
Om het snijpunt van beide grafieken te berekenen, moeten we de vergelijking:
![]()
oplossen.
We werken de vergelijking uit (zie verder bij het onderwerp Exponentiële vergelijkingen):
![]()
![]()
![]()
![]()
Om uit de tweede de derde vergelijking te krijgen, zijn beide leden met ![]() vermenigvuldigd, waardoor we een tweedegraads vergelijking in
vermenigvuldigd, waardoor we een tweedegraads vergelijking in ![]() krijgen, zie ook de onderwerpen Tweedegraads vergelijkingen (abc-formule) en Tweedegraads vergelijkingen (ontbinden in factoren).
krijgen, zie ook de onderwerpen Tweedegraads vergelijkingen (abc-formule) en Tweedegraads vergelijkingen (ontbinden in factoren).
We stellen nu een zogenaamde schaduwvergelijking op door te stellen:
![]()
We krijgen dan:
![]()
We kunnen deze vergelijking ontbinden in factoren:
![]()
De vergelijking heeft als oplossing:
![]() of
of ![]()
De eerste geeft geen oplossing voor ![]() want een standaard exponentiële functie kan niet negatief zijn. De andere oplossing levert:
want een standaard exponentiële functie kan niet negatief zijn. De andere oplossing levert:
![]()
![]()
Beide grafieken moeten elkaar dus snijden in ![]() , wat ook al werd gesuggereerd door de figuur.
, wat ook al werd gesuggereerd door de figuur.