Samenvatting en voorbeelden
De absolute waarde ![]() wordt vaak gezien als een lastige functie. Hij is als volgt gedefinieerd:
wordt vaak gezien als een lastige functie. Hij is als volgt gedefinieerd:
![]() als
als ![]()
![]() als
als ![]()
De absolute waarde geeft de grootte van ![]() weer, dus de waarde van
weer, dus de waarde van ![]() , maar dan zonder teken.
, maar dan zonder teken.
Voorbeeld 1
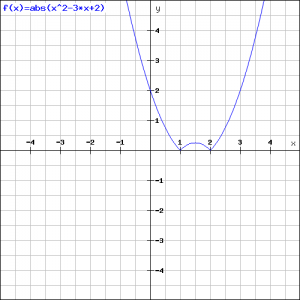
Als voorbeeld kijken we naar de functie ![]() . Volgens bovenstaande definitie is
. Volgens bovenstaande definitie is ![]() als
als ![]() , dus een rechte lijn en
, dus een rechte lijn en ![]() als
als ![]() .
.
Voorbeeld 2
Teken de grafiek van de functie:
![]()
Volgens de definitie geldt:
![]() als
als ![]() , we noemen dit geval A.
, we noemen dit geval A.
![]() als
als ![]() , we noemen dit geval B.
, we noemen dit geval B.
![]() als
als ![]() , we noemen dit geval C.
, we noemen dit geval C.
![]() als
als ![]() , we noemen dit geval D.
, we noemen dit geval D.
We beschouwen nu de volgende intervallen voor ![]() .
.
Als ![]() , dan gelden de gevallen B en D, dus:
, dan gelden de gevallen B en D, dus:
![]()
Als ![]() , dan gelden de gevallen B en C, dus:
, dan gelden de gevallen B en C, dus:
![]()
Als ![]() , dan gelden de gevallen A en C, dus:
, dan gelden de gevallen A en C, dus:
![]()
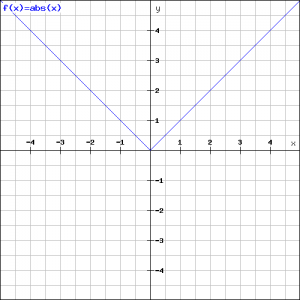
Dit resulteert in de volgende grafiek:
Voorbeeld 3
Nu de toepassing van de absolute waarde bij een tweedegraads functie:
![]()
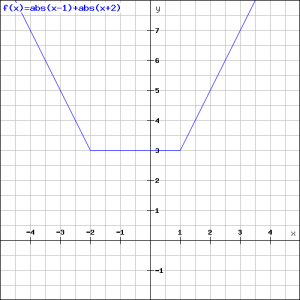
De grafiek van de functie ![]() is een parabool die de
is een parabool die de ![]() -as snijdt in
-as snijdt in ![]() en
en ![]() . De parabool is tevens een dalparabool en dus zal deze in het interval
. De parabool is tevens een dalparabool en dus zal deze in het interval ![]() beneden de
beneden de ![]() -as liggen. Omdat de functie
-as liggen. Omdat de functie ![]() de absolute waarde van deze parabool betreft, zal het negatieve deel worden vervangen door het positieve equivalent, zie de figuur.
de absolute waarde van deze parabool betreft, zal het negatieve deel worden vervangen door het positieve equivalent, zie de figuur.
Wanneer dit inzicht ontbreekt, kan natuurlijk ook de definitie van de absolute waarde worden toegepast:
![]() als
als ![]() of
of ![]()
![]() als
als ![]()