Return to Assignments Integration by substitution
Assignment 10
Solve:
![]()
Solution
We rewrite the integrand:
![]()
and the primitive is:
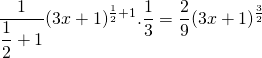
and thus the original integral becomes:
![]()
We can verify the result by differentiation. The chain rule has to be applied.
Return to Assignments Integration by substitution

