Assignments

In almost all applications of mathematics you need to be able to work with exponents. Whether the functions are root forms or fractions, you must always use a number of basic calculation rules. It is no less than a must to be able to apply these rules quickly. Learn them by heart and practice them with the following examples and assignments.

1. Simplify:

$\displaystyle\frac{L^{\alpha}K^{\beta}}{L}$

2. Simplify:

$\displaystyle\frac{4L^2K^3}{L^{-2}}$

3. Simplify:

$\displaystyle\frac{\displaystyle\frac{4(0.6)x^{0.4}y^{-0.4}}{y}}{\displaystyle\frac{4(0.4)x^{-0.6}y^{0.6}}{x}}$

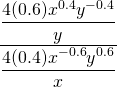
4. Simplify:

$\displaystyle\frac{2x^{0.25}y^{0.75}}{4x}$

5. Simplify:

$\displaystyle\frac{a^{x}\sqrt{a^{x}}}{3a^{1-x}}$

6. Simplify:

$\displaystyle\frac{y^5\sqrt{y^5}}{2y^{0.3}}$

7. Simplify:

$[-(-xy^3)^{-3}(x^6y^6)^2]^3$

8. Simplify:

$[(\displaystyle\frac{x}{2})^3\displaystyle\frac{8}{x^{-2}}]^{-3}$

9. Simplify:

$\displaystyle\frac{a^2b^{-\frac{1}{2}}\sqrt{c}}{a^{\frac{1}{2}}b^{-\frac{3}{2}}c}$

10. Simplify:

$\displaystyle\frac{{\sqrt[7]{{\frac{{a^2 b^{\frac{2}{3}} c^3 }}{{a^{} b^2 \sqrt a }}}}}}{{a^2 b^3 c}}$

0

Web Design Bangladesh Web Design Bangladesh Mymensingh