(Keller 7, 8, 9)
Probability distributions
(Keller 7, 8)
A probability distribution is a table, formula or graph that describes the values of a random variable and the probability associated with these values. Since a random variable can be either discrete or continuous we have two types of probability distributions: discrete and continuous probability distributions.
Example
The following formula represents the continuous normal distribution function.
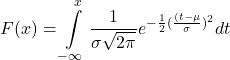
Example
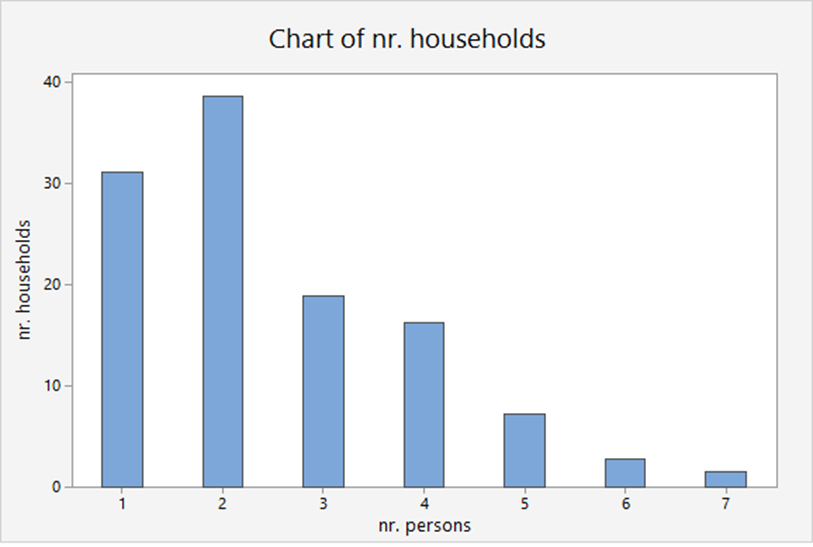
A distribution function can also be described by a table as is the case with the number of persons in a US household..
| Number of persons | Number of households |
|---|---|
| 1 | 31.1 |
| 2 | 38.6 |
| 3 | 18.8 |
| 4 | 16.2 |
| 5 | 7.2 |
| 6 | 2.7 |
| 7 or more | 1.4 |
| Total | 116.0 |
Discrete probability distributions
(Keller 7)
The following requirements hold for the probability ![]() :
:
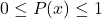 for all
for all 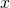 ;
;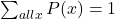 .
.
There is a relation between a relative frequency diagram and a discrete probability function.
Example
The probability distribution can be estimated from relative frequencies.
![]() is a discrete variable, the number of persons in a household.
is a discrete variable, the number of persons in a household.
| X | # households millions | P(x) |
| 1 | 31.1 | .268 |
| 2 | 38.6 | .333 |
| 3 | 18.8 | .162 |
| 4 | 16.2 | .140 |
| 5 | 7.2 | .062 |
| 6 | 2.7 | .023 |
| 7 or more | 1.4 | .012 |
| Total | 116.0 | 1.00 |
![]() is the discrete probability distribution of the number of persons in a household.
is the discrete probability distribution of the number of persons in a household.
We have: ![]() ,
, ![]() , etc.
, etc.
Also we can compute ![]()
Population mean E(X)
(Keller 7)
The population mean ![]() is the weighted average of all values of
is the weighted average of all values of ![]() . The weights are the probabilities.
. The weights are the probabilities.![]() is called the expected value of
is called the expected value of ![]() and is defined by the following formula.
and is defined by the following formula.
![]()
Example
What is the mean of throws of a fair dice?![]()
![]() for all
for all ![]() , because it is a fair dice.
, because it is a fair dice.
Applying the formula we get:
![]()
Population variance V(X)
(Keller 7)
The population variance ![]() is calculated similarly. It is the weighted average of the squared deviations from the mean
is calculated similarly. It is the weighted average of the squared deviations from the mean ![]() . The weights are the probabilities. It is defined by the following formula:
. The weights are the probabilities. It is defined by the following formula:
![]()
Example
We compute the variance of the households example. First we compute:
![]()
![]()
![]()
Now we can compute the variance:
![]()
![]()
![]()
The standard deviation is ![]() .
.
Covariance of two discrete variables
The covariance of two discrete variables ![]() and
and ![]() is defined as:
is defined as:
![]()
![]() is the joint probability distribution of the random variables
is the joint probability distribution of the random variables ![]() and
and ![]() :
: ![]() and
and ![]() .
.
Note. We also write ![]() .
.
Laws of E(X) and V(X)
(Keller 7)
The following formulas can easily be derived from the definitions of ![]() and
and ![]() .
.
![]()
![]()
![]()
![]()
![]()
![]()
For example: ![]()
Laws about a linear sum
(Keller, p. 234, ![]() and
and ![]() are two random variables).
are two random variables).
![]()
![]()
If ![]() and
and ![]() are independent then
are independent then ![]() and thus:
and thus:
![]()
Example
If ![]() and
and ![]() are independent then, because
are independent then, because ![]() and
and ![]() :
:![]()
![]()
Coefficient of correlation
The coefficient of correlation between two variables ![]() and
and ![]() is defined as the covariance divided by the standard deviations of the variables.
is defined as the covariance divided by the standard deviations of the variables.
The population coefficient of correlation is:
![]()
The sample coefficient of correlation is:
![]()
The coefficient of correlation answers the question: how strong is the association between ![]() and
and ![]() ?
?
The advantage of the coefficient of correlation over the covariance is that it has a fixed range from ![]() to
to ![]() (proven by Mathematics). If the two variables are very strongly and positively related, the coefficient value is close to
(proven by Mathematics). If the two variables are very strongly and positively related, the coefficient value is close to ![]() (strong positive linear relationship). If the two variables are very strongly and negatively related, the coefficient value is close to
(strong positive linear relationship). If the two variables are very strongly and negatively related, the coefficient value is close to ![]() (strong negative linear relationship). No straight linear relationship is indicated by a coefficient close to 0.
(strong negative linear relationship). No straight linear relationship is indicated by a coefficient close to 0.
The following graphs depict the relations of ![]() and
and ![]() for various coefficients of correlation, varying from
for various coefficients of correlation, varying from ![]() to
to ![]() . Below a number of examples.
. Below a number of examples.
Binomial distribution
(Keller 7)
The binomial distribution is the probability distribution that results from doing a binomial experiment. Binomial experiments have the following properties:
- There are a fixed number of trials, represented as
 ;
; - Each trial has two possible outcomes, success or failure;
 (success)
(success)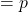 ;
; 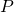 (failure
(failure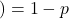 for all trials;
for all trials;- The trials are independent, meaning that the outcome of one trial does not affect the outcomes of any other trials.
The binomial random variable ![]() counts the number of successes in
counts the number of successes in ![]() trials of the binomial experiment.
trials of the binomial experiment.
(e.g. s s f s f f f s f s s f s shows ![]() trials and
trials and ![]() successes).
successes).
To calculate the probability associated with each value ![]() we use combinatorics:
we use combinatorics:
![]() for
for ![]()
Example
A quiz consists of ![]() independent multiple-choice
independent multiple-choice
questions (![]() ). Each question has
). Each question has ![]() possible answers, only one of which is correct (
possible answers, only one of which is correct (![]() ). You choose to guess the answer to each question.
). You choose to guess the answer to each question. ![]() is the number of correct guesses
is the number of correct guesses ![]() . The probability that you will have a score
. The probability that you will have a score ![]() is:
is:
![]()
{![]() is called
is called ![]() factorial
factorial ![]() ;
; ![]() ;
; ![]() ).
).
The mean, variance and standard deviation of a binomial random variable are (derived mathematically):
![]()
![]() and thus:
and thus:
![]()
Continuous random variables
(Keller 8)
Unlike a discrete random variable, a continuous random variable is one that assumes an uncountable number of values. We cannot list the possible values because there is an infinite number of them. Because there is an infinite number of values, the probability of each individual value is ![]() . The probability that a man has a height of exactly 180 cm is:
. The probability that a man has a height of exactly 180 cm is:
![]()
Pobability density functions
{Keller 8)
A function ![]() is called a probability density function (over the range
is called a probability density function (over the range ![]() ) if it meets the following requirements:
) if it meets the following requirements:
![]() for all
for all ![]()
and the total area between curve and ![]() -axis is:
-axis is:
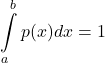
For the interval [a, b] we may also take ![]() , as is the case in e.g. the normal distribution.
, as is the case in e.g. the normal distribution.
The normal density function
(Keller 8)
The normal distribution is the most important of all probability distributions. The probability density function ![]() of a normal random variable
of a normal random variable ![]() is given by:
is given by:
![]() for
for ![]()
The graph is bell-shaped and symmetrical around the mean ![]() . This density function is also denoted by
. This density function is also denoted by ![]() or
or ![]() .
.
The normal distribution function is defined by:
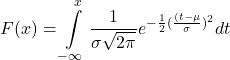
Therefore, the probability ![]() equals
equals ![]() .
.
This infinite integral cannot be computed analytically (pen and paper), therefore we need a table or a computer can do the job.
Standard normal distribution
(Keller 8)
A normal density function with mean ![]() and standard deviation
and standard deviation ![]() is called the standard normal density.
is called the standard normal density.
![]() for
for ![]()
Any normal distribution can be converted to a standard normal distribution, see below. The standard normal distribution is also denoted by ![]() . Any (normal) variable
. Any (normal) variable ![]() can be converted to a new (normal) variable
can be converted to a new (normal) variable ![]() :
:
![]()
with the following properties:
![]()
![]() .
.
Thus, if
![]()
then
![]() .
.
Example
Suppose the demand ![]() is a normally distributed variable with mean
is a normally distributed variable with mean ![]() and standard deviation
and standard deviation ![]() and we want to compute
and we want to compute ![]() . Then:
. Then:
![]()
![]()
![]() .
.
The answer can be found in Table 3 of Appendix B9 of Keller, or by Excel.
Other continuous distributions
There are three other continuous distributions which will be used and explained later.
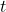 distribution (also called Student's
distribution (also called Student's 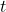 distribution);
distribution);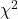 (Chi-squared) distribution;
(Chi-squared) distribution;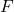 distribution.
distribution.