Summary and examples
To begin with there are some important rules for dealing with exponents. You will use them all the time and therefore you should learn them by heart.
Rules for exponents
![]()
Example: ![]()
![]()
Example: ![]()
![]()
Example: ![]()
![]()
Example: ![]()
![]()
Example: ![]()
![]()
![]()
![]()
![]()
Example: ![]()
Roots
There is much to say about roots, but you should know the following characteristics anyway.
![]() because
because ![]()
![]() because
because ![]()
![]() does not exist, because there is no real number that has
does not exist, because there is no real number that has ![]() as a square.
as a square.
![]() because
because ![]()
![]() because
because ![]()
![]() does not exist because there is no real number that has
does not exist because there is no real number that has ![]() as a result when it is raised to an even power.
as a result when it is raised to an even power.
Fractions
Adding and subtraction
We start with fractions containing only numbers. Fractions can be added or subtracted when the denominators of the fractions are equal. Note that a denominator is the expression below the vinculum ('divide by'); if the expression is not a denominator then it is a numerator.
![]()
We get equal denominators by multiplying the first denominator by ![]() and the second by
and the second by ![]() (you could say by multiplying the denominators). This is allowed if the numerators are multiplied by
(you could say by multiplying the denominators). This is allowed if the numerators are multiplied by ![]() and
and ![]() as well, respectively.
as well, respectively.
In the following example you would get equal denominators by multiplying by ![]() and
and ![]() . However, it is better to take the lowest common multiple of
. However, it is better to take the lowest common multiple of ![]() and
and ![]() and that is
and that is ![]() .
.
![]()
Usually we have to deal with fractions with letters. Look at the following example. We can make the denominators equal by multiplying the denominator of the first fraction by ![]() and the second denominator by
and the second denominator by ![]() . Of course, again: when both the denominator and numerator of a fraction are multiplied or divided by the same number
. Of course, again: when both the denominator and numerator of a fraction are multiplied or divided by the same number ![]() , the fraction retains the same value. See the following examples:
, the fraction retains the same value. See the following examples:
![]()
![]()
![]()
Multiplying and dividing
Calculate the following product of fractions:
![]()
Most students think this is not possible without a calculator. But when the above-mentioned rule is used, namely, that a fraction retains its value, when both numerator and denominator are multiplied or divided by the same number ![]() , it is easy to carry out the calculation.
, it is easy to carry out the calculation.
First we may write the fraction as follows:
![]()
Next we divide both numerator and denominator by common factors. As an example, if we divide both numerator and denominator by ![]() , then we get
, then we get ![]() in the numerator instead of
in the numerator instead of ![]() and in the denominator
and in the denominator ![]() instead of
instead of ![]() . Continuing in this way we get:
. Continuing in this way we get:
![]() .
.
Next we want to simplify the following fraction:
![]()
We may write (see the rules concerning exponents):
![]() en
en ![]()
resulting in:
![]()
Factorization and removing brackets
The following is an example of factorization.
![]()
The three terms in the left-hand side have the factors ![]() and
and ![]() in common and we want to use them as separate factors.
in common and we want to use them as separate factors.
Sometimes we want to remove brackets. The following two formulas are used frequently and need to be learned by heart.
![]()
![]()
There are a few cases that occur frequently and therefore must be learned by heart. They are known as special products. They are special because a product of two terms in generally yields four terms, but not in these cases. The result can be verified with the above formulas.
![]()
![]()
![]()
Linear functions and equations
A linear function (also called a first-degree function) has the following form:
![]()
The graph of this function is a straight line.
The parameters ![]() en
en ![]() have a special meaning.
have a special meaning.
The parameter ![]() is the slope of the line. When
is the slope of the line. When ![]() then the line is ascending (from bottom left to top right), in the case
then the line is ascending (from bottom left to top right), in the case ![]() the line descending (from top left to bottom right), when
the line descending (from top left to bottom right), when ![]() we are dealing with a horizontal line.
we are dealing with a horizontal line.
The parameter ![]() indicates the point where the line crosses the
indicates the point where the line crosses the ![]() -axis, namely in the point
-axis, namely in the point ![]() , because all points on the
, because all points on the ![]() -axis have the
-axis have the ![]() -coördinate
-coördinate ![]() .
.
When we want to find the point where the line crosses the ![]() -axis, we must choose
-axis, we must choose ![]() . After all, points on the
. After all, points on the ![]() -axis have a
-axis have a ![]() -coördinate
-coördinate ![]() .
.
![]() ,
, ![]() , so
, so ![]()
Solve the following linear equation, that is, find the value of ![]() for which the left and right side are equal.
for which the left and right side are equal.
![]()
Take the following steps.
step 1: remove left and right the brackets;
step 2: take left and right the ![]() -terms together; do the same with the numbers;
-terms together; do the same with the numbers;
step 3: place the ![]() -variable in the left side and the number in the right side;
-variable in the left side and the number in the right side;
step 4: make sure that the result looks like this: ![]() .
.
Example 1
step 1: ![]()
step 2: ![]()
step 3: ![]()
step 4: ![]()
Example 2
Sometimes a linear equation is disguised as a higher degree equation.
Look at the following example:
![]()
In simplifying the third power and the square disappear and a linear equation remains:
![]()
![]()
![]()
Liner inequalities
It is important to remember that the inequality sign of an inequality turns around as left and right side are multiplied by the same negative number.
Example 3
![]()
![]()
![]()
Example 4
![]()
This inequality can be rewritten as:
![]()
Multiply left and right side by ![]() and the inequality sign will be
and the inequality sign will be ![]() instead of
instead of ![]() so:
so:
![]()
Quadratic or second degree equations
The general formula is:
![]()
(![]() , if
, if ![]() then we do not have a quadratic function).
then we do not have a quadratic function).
The graph is a parabola; if ![]() :
: ![]() (opens up);
(opens up); ![]() :
: ![]() (opens down).
(opens down).
The number ![]() determines the intersection point of the parabola with the
determines the intersection point of the parabola with the ![]() -as. After all, all points on the
-as. After all, all points on the ![]() -axis have the coordinate
-axis have the coordinate ![]() and thus
and thus ![]() is the intersecion point of the graph with the
is the intersecion point of the graph with the ![]() -axis.
-axis.
To find the intersection points with the ![]() -axis (i.e.,
-axis (i.e., ![]() ) you have to solve the equation:
) you have to solve the equation: ![]() .
.
This equation has not always (real) solutions. An 'opens up' parabola with a minimum above the ![]() -axis and an 'opens down' parabola with a maximum below the
-axis and an 'opens down' parabola with a maximum below the ![]() -axis do not have intersection points with the
-axis do not have intersection points with the ![]() -axis. Whether the graph of a parabola will cross the
-axis. Whether the graph of a parabola will cross the ![]() -axis, depends on the discriminant
-axis, depends on the discriminant ![]() , see below.
, see below.
How do we solve a quadratic equation ![]() ?
?
We distinguish the following methods:
- Factorization (sometimes that is easy to do and then this method is preferred, but this is not always the case);
- The
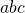 -formula (always delivers a solution if one exists);
-formula (always delivers a solution if one exists); - Special cases.
The quadratic formula definitely delivers a solution if one exists, but the other methods are sometimes faster to calculate.
Factorization
Try the expression ![]() to write in the form
to write in the form ![]() . where
. where ![]() and
and ![]() are whole numbers which have
are whole numbers which have ![]() as a product and
as a product and ![]() as a sum (the so-called sum-product method).
as a sum (the so-called sum-product method).
Example 5
![]() can be written as
can be written as ![]() for
for ![]() and
and ![]()
![]() can be written as
can be written as ![]() for
for ![]() and
and ![]()
This method is only easy to use if ![]() . If
. If ![]() left and right side are divided by
left and right side are divided by ![]() . However, when because of this operation one of the coefficients will become a fraction, the sum-product method will not be used.
. However, when because of this operation one of the coefficients will become a fraction, the sum-product method will not be used.
abc-formula
The solution of the quadratic equation ![]() can be found by using the following formula.
can be found by using the following formula.
![]()
This formula is known as the ![]() -formula.
-formula. ![]() is the discriminant:
is the discriminant: ![]() .
.
There are three possibilities:
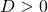 : 2 different solutions
: 2 different solutions 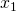 or
or 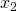
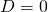 : 1 solution (actually 2 equal solutions
: 1 solution (actually 2 equal solutions 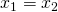 )
)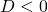 : no (real) solutions
: no (real) solutions
Example 6
![]()
so:
![]()
So the solutions are: ![]() of
of ![]() .
.
This equation can also be solved with the sum-product method. Try!
![]()
so
![]()
So the solutions are ![]() of
of ![]()
Special cases
The first case is when ![]() .
.
![]() , so
, so ![]() , and so
, and so ![]() of
of ![]() (do not forget the minus solution).
(do not forget the minus solution).
In the other case we have ![]() .
.
Then we just get ![]() outside brackets.
outside brackets.
![]() , so
, so ![]() and so
and so ![]() of
of ![]() .
.

