Return to Assignments Addition and subtraction formulas
Assignment 1
Show:
![]()
Solution
In the right-hand side we substitute:
![]()
and get:
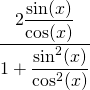
We multiply both numerator and denominator by ![]() :
:
![]()
Return to Assignments Addition and subtraction formulas
Show:
![]()
In the right-hand side we substitute:
![]()
and get:
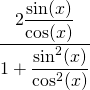
We multiply both numerator and denominator by ![]() :
:
![]()