Logaritmische functies en grafieken

Samenvatting en voorbeelden

De logaritmische functie en de exponentiële functie zijn elkaars inversen. In Nederland is het de gewoonte de logaritmsche functie te schrijven als:

$y= ^g\log(x)$

dat wil zeggen met het zogenaamde grondtal $g$ linksboven. Elders, met name in de Angelsaksische landen wordt de logaritme geschreven als:

$y=\log_b(x)$

waarin de $b$ staat voor base. We zullen in het vervolg de laatste schrijfwijze hanteren maar wel de $g$ handhaven. Vaak wordt de logaritme geschreven zonder haakjes rondom het argument. Wij kiezen ervoor wel de haakjes te gebruiken om verwarring te voorkomen.

De logaritmische functie is derhalve:

$y=\log_g(x)$

onder de volgende voorwaarden:

$g>0$ en $g\neq1$

$x>0$

Om deze voorwaarden te begrijpen, kan de volgende definitie van de logaritme worden gebruikt:

$y=\log_g(x)\Longleftrightarrow x=g^y$

Met behulp van deze formule kunnen logaritmen soms snel worden berekend.

Voorbeeld 1

Bereken:

$\log_{10}(100)$

Volgens bovenstaande relatie kunnen we hiervoor schrijven:

$y=\log_{10}(100)\Longleftrightarrow 100=10^y$

en we zien onmiddellijk dat $y=2$ de oplossing is.

Voorbeeld 2

Bereken:

$\log_3(27)$

Volgens bovenstaande definitie kunnen we hiervoor schrijven:

$y=\log_3(27)\Longleftrightarrow 27=3^y$

en we zien onmiddellijk dat $y=3$ de oplossing is.

Voorbeeld 3

Bereken:

$\log_4(\displaystyle\frac{1}{64})$

Volgens bovenstaande definitie kunnen we hiervoor schrijven:

$y=\log_4(\displaystyle\frac{1}{64})\Longleftrightarrow \displaystyle\frac{1}{64}=4^y$

We herschrijven:

$4^y=\displaystyle\frac{1}{64}=\displaystyle\frac{1}{4^3}=4^{-3}$

en dus is de oplossing $y=-3$ .

Voorbeeld 4

Bereken:

$\log_\frac{1}{2}(16)$

Volgens bovenstaande definitie kunnen we hiervoor schrijven:

$y=\log_\frac{1}{2}(16)\Longleftrightarrow 16=(\frac{1}{2})^y=(2^{-1})^y=2^{-y}$

Dus:

$2^{-y}=16=2^4$

en dus is de oplossing:

$y=-4$

Over het grondtal $g$ nog twee opmerkingen.

Wanneer het grondtal wordt weggelaten, dan wordt aangenomen dat 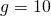$g=10$ ; we schrijven dan $\log(x)$ .
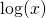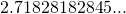Wanneer het grondtal het getal $e$ is (het getal van Euler, $2.71828182845...$ ), dan wordt in plaats van 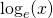$\log_e(x)$ geschreven 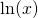$\ln(x)$ . We noemen een dergelijke logaritme een natuurlijke logaritme.

Er zijn vier formules die bij het werken met logaritmen veel worden gebruikt. Het is handig die altijd paraat te hebben en hiervoor niet steeds naar een boek te hoeven grijpen.
Het zijn de volgende formules:

$\log_g(ab)=\log_g(a)+\log_g(b)$
$\log_g(\displaystyle\frac{a}{b})=\log_g(a)-\log_g(b)$
$\log_g(a^n)=n\log_g(a)$
$\log_g(a)=\displaystyle\frac{\log_c(a)}{\log_c(g)}$

Voor $c$ gelden dezelfde voorwaarden als voor $g$ . Over deze formules moeten we nog enkele opmerkingen maken. Ze komen niet zomaar uit de lucht vallen, maar kunnen met behulp van de definitie worden afgeleid. Verder zien we dat de derde formule rechtstreeks volgt uit de eerste. De laatste formule geldt voor elke $c$ die voldoet aan eerdergenoemde voorwaarden voor het grondtal. Het nut van deze formule is groot, zo zal iedere gebruiker van een rekenmachine beamen. Wanneer iemand zijn steun en toeverlaat wil gebruiken om de volgende logaritme te berekenen:

$\log_5(7)$

zal hij vergeefs zoeken naar de toets die voor de logaritme met grondtal $5$ kan worden gebruikt. Wel zal hij de $\log$ -toets opmerken (grondtal $10$ ) en de $\ln$ -toets (grondtal $e$ ), maar niet een toets voor de log met grondtal $5$ . Door de vierde formule te gebruiken, lukt het hem wel het antwoord te berekenen:

$\log_5(7)=\displaystyle\frac{\log(7)}{\log(5)}\approx1.21$

Voorbeeld 5

Los op:

$\ln(x^2)+3\ln(x)=10$

We schrijven met behulp van de derde formule:

$2\ln(x)+3\ln(x)=10$

$5\ln(x)=10$

$\ln(x)=2$

$x=e^2$

De grafiek van de logaritmische functie:

$y=\log_g(x)$

hangt af van het grondtal $g$ . In onderstaande figuur zien we de grafieken van:

$l_1: y=\log_3(x)$

$l_2: y=\log_\frac{1}{3}(x)$

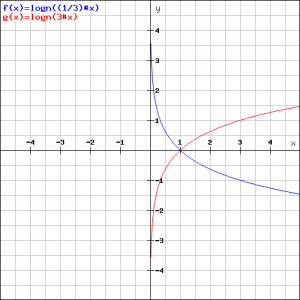
De blauwe grafiek hoort bij $l_1$ , de rode bij $l_2$ . Toon met behulp van de definitie aan dat $l_1$ en $l_2$ elkaars gespiegelde zijn in de $X$ -as.
We zien dat de beide grafieken door het punt $(1,0)$ gaan. Dat is het geval voor alle toegestane grondtallen.