Samenvatting en voorbeelden
Een tweedegraads vergelijking, dus van het type:
komt alleen in aanmerking voor een aanpak met behulp van ontbinden in factoren wanneer aan de volgende voorwaarden wordt voldaan:
, 
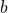en 
zijn gehele getallen;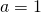
; wanneer 
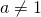moet het niet mogelijk zijn door deling 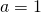te maken zonder dat de andere coëfficiënten breuken worden.
Wanneer deze aanpak niet tot resultaten leidt, moet de abc-formule worden toegepast, zie het onderwerp Tweedegraads vergelijkingen (abc-formule).
We zullen het voorgaande aan de hand van een het volgende voorbeeld toelichten.
Voorbeeld 1
Van de volgende voorbeelden wordt aangegeven of het zinvol is de vergelijking te ontbinden in factoren en waarom.
a. 
Ja. , en zijn gehele getallen en voor de coëfficiënt geldt .
b. 
Nee. , en zijn weliswaar gehele getallen, maar voor de coëfficiënt geldt en delen door 
geeft coëfficiënten met een breuk.
c. 
Ja. In eerste instantie 'neen', want , en zijn weliswaar gehele getallen, maar . Echter, delen door geeft de vergelijking:
en die voldoet weer aan de voorwaarden. Dus toch 'ja'.
Hoe lossen we een tweedegraads vergelijking op met ontbinden in factoren? Laten we dit toelichten aan de hand van een voorbeeld.
Probeer de vergelijking:
te schrijven in de vorm:
waarin 
en 
gehele getallen zijn.
We moeten en zien te vinden zodanig dat de vergelijking:
gelijk is aan de vergelijking:
Dit is het geval wanneer en voldoen aan de volgende twee voorwaarden:
en
Het is even puzzelen, maar je ziet al gauw dat 
en 
voldoen. Om deze waarden snel te vinden begin je met het product. Kijk dus eerst naar welke gehele getallen met elkaar vermenigvuldigd het antwoord 
opleveren. Mogelijkheden zijn: 
en 
; en . Daarna kijk je of de gevonden waarden opgeteld de som 
opleveren. De eerste mogelijkheid voldoet niet, de tweede wel. Wanneer voor en geen gehele waarden kunnen worden gevonden die aan de voorwaarden voldoen, dan moet de vergelijking worden opgelost met de abc-formule.
De vergelijking:
kan dus worden geschreven als:
Ga dit na met behulp van de 'bananenformule':
We moeten dus nu de vergelijking oplossen:
De oplossingen zijn:
of 
Dit levert de oplossingen van de vergelijkingen:
of 
Wanneer je er meer ervaring mee hebt, kun je een tweedegraads vergelijking vaak snel met ontbinden in factoren oplossen. Wie liever de abc-formule wil toepassen is vaak wat langer bezig, moet wat meer berekeningen maken, maar vindt de oplossingen altijd (wanneer hij tenminste geen fouten maakt).
Voorbeeld 2
Los op:
We moeten dus en vinden zodanig dat:
en 
Hieraan voldoen:
en
Dus de vergelijking kan worden geschreven als:
en dus zijn de oplossingen:
of 
Voorbeeld 3
Los op:
Er moet dus gelden:
en 
Hieraan voldoen:
en 
Dus de vergelijking kan worden geschreven als:
en dus zijn de oplossingen:
of 
Voorbeeld 4
Los op:
Er moet dus gelden:
en 
Hieraan voldoen:
en 
Dus de vergelijking kan worden geschreven als:
en dus zijn de oplossingen:
of
Voorbeeld 5
Los op:
Er moet dus gelden:
en 
Hieraan voldoen:
en 
Dus de vergelijking kan worden geschreven als:
en dus zijn de oplossingen:
of
Voorbeeld 6
Los op:
Er moet dus gelden:
en 
Er zijn geen gehele getallen en die aan deze vergelijkingen voldoen. Dit wil niet zeggen dat de vergelijking geen oplossingen heeft. In dit geval heeft de vergelijking wel oplossingen en om die te vinden moet de abc-formule worden gebruikt (zie daartoe het onderwerp Tweedegraads vergelijkingen (abc-formule).
Voorbeeld 7
Los op:
Er moet dus gelden:
en
Er zijn geen gehele getallen en die aan deze vergelijkingen voldoen. Dit wil niet zeggen dat de vergelijking geen oplossingen heeft, maar in dit geval heeft deze vergelijking inderdaad geen oplossingen (bij het onderwerp Tweedegraads vergelijkingen (abc-formule) blijkt dat de discriminant van deze vergelijking kleiner dan nul is en dan heeft de vergelijking geen reële oplossingen).
