Tweedegraads functies en grafieken

Samenvatting en voorbeelden

De algemene vergelijking van een tweedegraads functie is:

$y=ax^2+bx+c$

$a$ , $b$ en $c$ zijn parameters. Voor $a$ moet gelden $a\neq0$ , anders is er geen sprake van een tweedegraads functie.

De grafiek van een tweedegraads functie is een parabool. Er zijn twee typen parabolen, de dal- en bergparabool.

Er geldt:

$a>0$ : dalparabool

$a<0$ : bergparabool

Een parabool snijdt de $Y$ -as in het punt $(0,c)$ . Dat kunnen we snel zien, want voor elk punt op de $Y$ -as geldt $x=0$ . Wanneer $x=0$ in de vergelijking wordt gesubstitueerd, krijgen we $y=c$ .

Wanneer een parabool de $X$ -as snijdt kunnen de snijpunten op diverse manieren worden gevonden. De $abc$ -formule, behandeld in het onderwerp Tweedegraads vergelijkingen (abc-formule), leidt altijd tot een oplossing, maar ook kan worden geprobeerd het rechter lid te ontbinden in factoren, zie het onderwerp Tweedegraads vergelijkingen (ontbinden in factoren).
De snijpunten kunnen worden berekend met behulp van de $abc$ -formule:

$x_{1,2}=\displaystyle\frac{-b\pm\sqrt{b^2-4ac}}{2a}$

In deze formule speelt de discriminant een belangrijke rol:

$D=b^2-4ac$

Immers, er geldt:

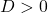$D>0$ : de parabool heeft twee verschillende snijpunten met de 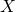$X$ -as;
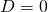$D=0$ : de parabool heeft twee samenvallende snijpunten met de 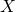$X$ -as (ook wordt wel gezegd dat de parabool dan slechts een snijpunt heeft); en
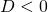$D<0$ : de parabool heeft geen snijpunten met de $X$ -as.

Een parabool is een symmetrische figuur is en heeft een symmetrie-as, namelijk de lijn:

$x=-\displaystyle\frac{b}{2a}$

Het spreekt vanzelf dat de top van een parabool op deze symmetrie-as ligt:

$x_{top}=-\displaystyle\frac{b}{2a}$

Dat dit zo is, kan ook uit de $abc$ -formule worden afgeleid. Ook kan deze waarde worden gevonden door de afgeleide van de functie gelijk aan $0$ te stellen:

$y'=2ax+b=0$
$x=-\displaystyle\frac{b}{2a}$

met de bedoeling de extreme waarde te berekenen, zie ook het onderwerp Differentiëren van standaardformules .

Voorbeeld 1

Gegeven de functie:

$y=3x^2+2x-1$

Beantwoord de volgende vragen:

1. Wat is het snijpunt van de grafiek met de $Y$ -as;
2. Heeft deze grafiek snijpunten met de $X$ -as, en zo ja, hoeveel en bepaal de coördinaten van deze snijpunten.
3. Bepaal de symmetrie-as.

1. Omdat de $c$ in de formule gelijk is aan $-1$ , is het snijpunt met de $Y$ -as gelijk aan $(0,-1)$ .
2. Om na te gaan of de grafiek van de functie snijpunten heeft met de $X$ -as, moet de discriminant worden berekend:

$D=2^2-4.3.-1=16$

De discriminant $D$ is groter dan $0$ en dus heeft de grafiek twee snijpunten met de $X$ -as. De $x$ -coördinaten van deze snijpunten zijn:

$\displaystyle\frac{-2\pm\sqrt{16}}{2.3}=\displaystyle\frac{-2\pm4}{6}$

dus:

$x_1=-1$
$x_2=\displaystyle\frac{1}{3}$

en dus zijn de coördinaten:

$(-1,0)$ en $(\displaystyle\frac{1}{3},0)$

3. De symmetrie-as kan op twee manieren worden berekend. In de eerste plaats door de bovengenoemde formule te gebruiken, maar ook door het midden te nemen van de snijpunten met de $X$ -as, namelijk:

$x=\displaystyle\frac{-1+\displaystyle\frac{1}{3}}{2}=-\displaystyle\frac{1}{3}$

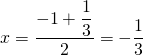
Voorbeeld 2

Gegeven de functie:

$y=x^2-6x+8$

Beantwoord de volgende vragen:

1. Wat is het snijpunt van de grafiek met de $Y$ -as;
2. Heeft deze grafiek snijpunten met de $X$ -as, en zo ja, hoeveel en bepaal de coördinaten.
3. Bepaal de symmetrie-as.

1. Omdat de $c$ in de formule gelijk is aan $8$ , is het snijpunt met de $Y$ -as gelijk aan $(0,8)$ .
2. Om na te gaan of de grafiek van de functie snijpunten heeft met de $X$ -as, moet de discriminant worden berekend. maar we kunnen dat ook op een andere manier doen. We kunnen namelijk constateren dat de vergelijking kan worden ontbonden in factoren: