Rekenregels voor exponenten

Samenvatting en voorbeelden

Het rekenen met exponenten is een van de meest voorkomende bewerkingen in de wiskunde en in de meest uiteenlopende toepassingen. Het is daarom zaak om de volgende rekenregels voor exponenten uitstekend te beheersen.

$a^p.a^q=a^{p+q}$
$\displaystyle\frac{a^p}{a^q}=a^{p-q}$
$(ab)^p=a^pb^p$
$(\displaystyle\frac{a}{b})^p=\frac{a^p}{b^p}$
$(a^p)^q=a^{pq}$
$a^p=\displaystyle\frac{1}{a^{-p}}$
$a^{-p}=\displaystyle\frac{1}{a^p}$
$a^0=1$
$a^1=a$
$\sqrt[q]{a^p}=a^{\frac{p}{q}}$

Er moeten hierbij nog enkele opmerkingen worden gemaakt.
De bewerkingen 6 en 7 kunnen zo worden begrepen: een machtsfunctie in de teller kan naar de noemer worden verplaatst maar dan wisselt de exponent van teken. Dit geldt ook voor een machtsfunctie die van noemer naar teller gaat.
Om de een of andere manier zijn leerlingen of studenten vaak van mening dat $a^0=0$ is, maar dat is fout. Het juiste antwoord kan met behulp van 2. worden bewezen wanneer $p=q$ wordt gekozen.
Aan de hand van de voorbeelden kan men nagaan hoe goed men de rekenregels voor exponenten beheerst.
N.B. Tenslotte nog een opmerking. Vaak wordt het niet netjes gevonden een gebroken exponent te laten staan maar in plaats hiervan een wortelfunctie te plaatsen. Hier wordt deze fatsoensregel niet altijd nageleefd.

Voorbeeld 1

Vereenvoudig:

$(27x^3y^6)^\frac{1}{3}$

Deze expressie kan worden geschreven als:

$(3^3)^{\frac{1}{3}}(x^3)^{\frac{1}{3}}(y^6)^{\frac{1}{3}}=3xy^2$

Voorbeeld 2

Vereenvoudig:

$((c^{\frac{1}{2}})^{\frac{2}{3}})^{\frac{3}{4}}$

Deze expressie kan worden geschreven als:

$((c^{\frac{1}{2}})^{\frac{2}{3}})^{\frac{3}{4}}=c^{\frac{1}{2}.\frac{2}{3}.\frac{3}{4}}=c^{\frac{1}{4}}=\sqrt[4]{c}$

Voorbeeld 3

Vereenvoudig:

$\displaystyle\frac{16\sqrt[3]{x^2}\sqrt[4]{y}\sqrt{\frac{1}{z}}}{4\sqrt[3]{x}\sqrt{y^5}\sqrt{z}}$

Deze expressie kan worden geschreven als:

$\displaystyle\frac{16x^{\frac{2}{3}}y^{\frac{1}{4}}z^{-\frac{1}{2}}}{4x^{\frac{1}{3}}y^{\frac{5}{2}}z^{\frac{1}{2}}}=4x^{\frac{1}{3}}y^{-\frac{9}{4}}z^{-1}=4\displaystyle\frac{\sqrt[3]{x}}{y^2z\sqrt[4]{y}}$

Voorbeeld 4

Vereenvoudig:

$(\displaystyle\frac{10p^{-1}q^{\frac{2}{3}}}{40p^2q^{\frac{7}{3}}})^{-\frac{2}{3}}$

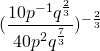
Deze expressie kan worden geschreven als:

$(\displaystyle\frac{1}{4}p^{-3}q^{-\frac{5}{3}})^{-\frac{2}{3}}=4^{\frac{2}{3}}p^2q^{\frac{10}{9}}$