Samenvatting en voorbeelden
In de onderstaande figuur is de grafiek van de functie ![]() getekend voor het interval
getekend voor het interval ![]() (de figuur is ontleend aan Wikipedia).
(de figuur is ontleend aan Wikipedia).
Stel dat we de oppervlakte willen uitrekenen van deze figuur die begrensd wordt door ![]() ,
, ![]() en
en ![]() . Omdat we (nog) niet weten hoe je een oppervlakte uitrekent met een gekromde begrenzing (in dit geval
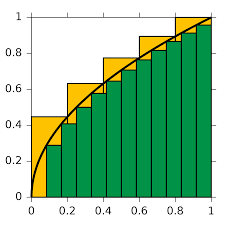
. Omdat we (nog) niet weten hoe je een oppervlakte uitrekent met een gekromde begrenzing (in dit geval ![]() ) zouden we kunnen kiezen voor de volgende aanpak. We benaderen de gewenste oppervlakte door de oppervlakten van de gele rechthoeken uit te rekenen en op te tellen:
) zouden we kunnen kiezen voor de volgende aanpak. We benaderen de gewenste oppervlakte door de oppervlakten van de gele rechthoeken uit te rekenen en op te tellen:
![]()
Op deze manier benaderen we de oppervlakte 'van boven', immers de som van de oppervlakten van de gele rechthoeken is groter dan de oppervlakte waarvan we de grootte willen bepalen. We zouden ook kunnen uitgaan van de groene rechthoeken, maar dan benaderen we de gewenste oppervlakte 'van onder'.
We zien echter dat in beide gevallen de gekozen benadering te grof is en dus kiezen we een nauwkeuriger benadering door de breedte van de rechthoeken gelijk aan ![]() te kiezen. Ook deze benadering is nog niet goed genoeg en daarom kiezen we de breedte van de rechthoeken gelijk aan
te kiezen. Ook deze benadering is nog niet goed genoeg en daarom kiezen we de breedte van de rechthoeken gelijk aan ![]() waarbij
waarbij ![]() , dat wil zeggen voor steeds kleinere waarden van
, dat wil zeggen voor steeds kleinere waarden van ![]() . Let op: gewoon kiezen voor
. Let op: gewoon kiezen voor ![]() levert als resultaat
levert als resultaat ![]() op en dat is zeker niet de uitkomst. De oppervlakte kan nu als volgt worden berekend:
op en dat is zeker niet de uitkomst. De oppervlakte kan nu als volgt worden berekend:
Oppervlakte=![]()
In het bovenstaande voorbeeld geldt:
![]()
Voor de ingewikkelde formule schrijven we kortheidshalve:
Oppervlakte=![Rendered by QuickLaTeX.com \displaystyle\lim_{\Delta{x}\rightarrow0}\sum_{\forall{x_{i}}\in[0,1]}f(x_{i})\Delta{x}=\int_{0}^{1}f(x)dx](https://4mules.nl/wp-content/ql-cache/quicklatex.com-92b77951b0319337280afbf5ee333521_l3.png)
De verkorte schrijfwijze heet een bepaalde integraal tussen de grenzen ![]() en
en ![]() . De
. De ![]() is de ‘oneindig kleine’ versie van
is de ‘oneindig kleine’ versie van ![]() .
.
In het onderwerp Integreren van standaardfuncties wordt toegelicht hoe we de bepaalde integraal kunnen uitrekenen.
In dit onderdeel kijken we slechts naar de berekening van oppervlakten en concluderen uit het bovenstaande dat integreren ons hierbij kan helpen. Later zullen we zien dat we met behulp van integralen ook inhouden kunnen berekenen, met name van omwentelingslichamen.
Voordat we verder gaan met de details van het berekenen van oppervlakten met behulp van integreren, maken we nog even bovenstaande integraal af.
In het onderdeel Integreren van standaardfuncties zien we dat de primitieve functie van:
![]()
is
![]()
en dus geldt:
![]()
Er moeten nog enkele opmerkingen worden gemaakt. In het bovenstaande geval ligt de grafiek van ![]() en dus ook het ingesloten gebied boven de
en dus ook het ingesloten gebied boven de ![]() -as. Wanneer voor een andere functie de grafiek en dus ook het ingesloten gebied onder de
-as. Wanneer voor een andere functie de grafiek en dus ook het ingesloten gebied onder de ![]() -as zou liggen, zou de integraal een negatieve uitkomst hebben gegeven. Immers,
-as zou liggen, zou de integraal een negatieve uitkomst hebben gegeven. Immers, ![]() is weliswaar positief, maar de opeenvolgende waarden
is weliswaar positief, maar de opeenvolgende waarden ![]() zouden alle negatief zijn en dus ook het resultaat van de integraal.
zouden alle negatief zijn en dus ook het resultaat van de integraal.
Voorbeeld 1
Bereken de oppervlakte van het gebied dat ligt tussen ![]() en de
en de ![]() -as, tussen
-as, tussen ![]() en
en ![]() .
.
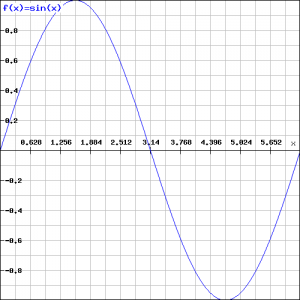
Argeloos zouden we deze oppervlakte als volgt kunnen berekenen, maar het resultaat wekt wel verbazing:
![]()
Dit vreemde resultaat klopt natuurlijk niet. Dit is te verklaren uit het feit dat de 'positieve' oppervlakte van het ingesloten gebied boven de ![]() -as wordt gecompenseerd door de ‘negatieve’ oppervlakte van het ingesloten onder de
-as wordt gecompenseerd door de ‘negatieve’ oppervlakte van het ingesloten onder de ![]() -as.
-as.
Het juiste resultaat zouden we kunnen krijgen door uit te rekenen:
Oppervlakte![]()
Voorbeeld 2 (Inhoud van omwentelingslichamen)
Wanneer we de grafiek van ![]() (zie hierboven) om de
(zie hierboven) om de ![]() -as wentelen krijgen we een paraboloïde (figuur afkomstig van www.math4all.nl). In de onderstaande figuur zien we dat er een omwentelingsvlak ontstaat, in dit geval voor
-as wentelen krijgen we een paraboloïde (figuur afkomstig van www.math4all.nl). In de onderstaande figuur zien we dat er een omwentelingsvlak ontstaat, in dit geval voor ![]() .
.
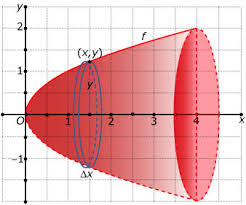
Wat zouden we nu kunnen doen om de inhoud van dit omwentelingslichaam te berekenen.
We gaan als volgt te werk. Stel dat we ter hoogte van ![]() een cirkel trekken met straal
een cirkel trekken met straal ![]() . Wanneer we op basis hiervan een cilinder maken met een dikte (of hoogte)
. Wanneer we op basis hiervan een cilinder maken met een dikte (of hoogte) ![]() is de inhoud van dit schijfje
is de inhoud van dit schijfje ![]() . De gevraagde inhoud kan nu worden benaderd door de inhoud van alle schijfjes op te tellen en vervolgens
. De gevraagde inhoud kan nu worden benaderd door de inhoud van alle schijfjes op te tellen en vervolgens ![]() steeds kleiner te kiezen,
steeds kleiner te kiezen, ![]() :
:
Inhoud =![Rendered by QuickLaTeX.com \displaystyle\lim_{\Delta{x}\rightarrow0}\sum_{\forall{x_{i}}\in[0,4]}\pi{y^2}\Delta{x}=\int_{0}^{4}\pi{y^2}dx](https://4mules.nl/wp-content/ql-cache/quicklatex.com-4d6a6f78c5063f7eb5cf030c76eb3090_l3.png)
In dit geval geldt ![]() en dus krijgen we:
en dus krijgen we:
Inhoud ![]()
Wanneer we de grafiek om de ![]() -as zouden hebben gewenteld, bijvoorbeeld tussen
-as zouden hebben gewenteld, bijvoorbeeld tussen ![]() en
en ![]() , verloopt de berekening nagenoeg op dezelfde wijze (merk op
, verloopt de berekening nagenoeg op dezelfde wijze (merk op ![]() ).
).
Inhoud =![]()
![]()
Voorbeeld 3
Bepaal de inhoud van een kegel met straal ![]() en hoogte
en hoogte ![]() . Tot voor kort moesten we genoegen nemen met de aankondiging dat geldt:
. Tot voor kort moesten we genoegen nemen met de aankondiging dat geldt:
Inhoud ![]()
dat wil zeggen, de inhoud is een derde maal de oppervlakte van de grondcirkel keer de hoogte. Hieronder zullen we zelf nagaan dat deze formule klopt.
We construeren de gewenste kegel door een rechte lijn om de ![]() -as te wentelen. We moeten dan gebruik maken van de volgende lijn:
-as te wentelen. We moeten dan gebruik maken van de volgende lijn:
![]()
en zien dat deze lijn gaat door de punten ![]() en
en ![]() . Omwenteling van deze lijn rond de
. Omwenteling van deze lijn rond de ![]() -as levert de gewenste kegel op: een grondcirkel met straal
-as levert de gewenste kegel op: een grondcirkel met straal ![]() en een hoogte
en een hoogte ![]() .
.
Om de inhoud te berekenen, gebruiken we dus de formule:
Inhoud =![]()
Voor ![]() geldt:
geldt:
![]()
en dus:
Inhoud = ![]()

