Samenvatting en voorbeelden
Een eenvoudig voorbeeld van een gebroken functie is de volgende functie:
![]()
Vanzelfsprekend geldt een beperkende voorwaarde voor ![]() :
:
![]()
Voor de waarde ![]() heeft de functie een verticale asymptoot.
heeft de functie een verticale asymptoot.
Er bestaat ook een horizontale asymptoot. Dat is de lijn die de grafiek nadert wanneer ![]() of
of ![]() . In dit geval zal de grafiek de lijn
. In dit geval zal de grafiek de lijn ![]() naderen, omdat de breuk in die gevallen tot
naderen, omdat de breuk in die gevallen tot ![]() zal naderen.
zal naderen.
Voorbeeld 1
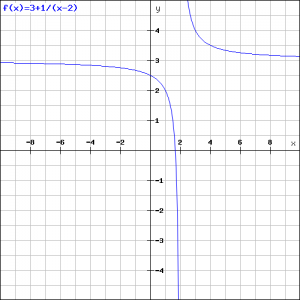
Laten we als eerste voorbeeld de functie nemen met ![]() ,
, ![]() en
en ![]() . De grafiek ziet er als volgt uit:
. De grafiek ziet er als volgt uit:
Om deze grafiek goed te kunnen schetsen, is het verstandig de volgende stappen te volgen:
- Bepaal de verticale asymptoot (in dit geval
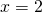 );
); - Bepaal de horizontale asymptoot (in dit geval
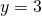 );
); - Bepaal het snijpunt met de
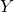 -as, indien het bestaat;
-as, indien het bestaat; - Bepaal het snijpunt met de
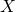 -as, indien het bestaat;
-as, indien het bestaat;
De verticale en horizontale asymptoten zijn snel gevonden. Ook het snijpunt met de ![]() -as levert geen problemen op (kies
-as levert geen problemen op (kies ![]() en we vinden
en we vinden ![]() ). Het snijpunt met de
). Het snijpunt met de ![]() -as vinden we door de volgende vergelijking op te lossen:
-as vinden we door de volgende vergelijking op te lossen:
![]()
![]()
Voorbeeld 2
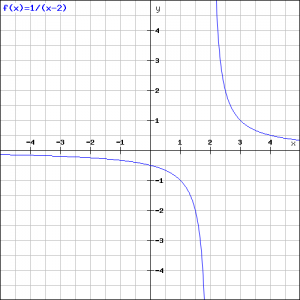
Bepaal van de functie:
![]()
de verticale asymptoot;
de horizontale asymptoot;
het snijpunt met de ![]() -as als dat bestaat;
-as als dat bestaat;
het snijpunt met de ![]() -as als dat bestaat.
-as als dat bestaat.
Schets met behulp van deze resultaten de grafiek.
We zien onmiddellijk dat de verticale asymptoot is ![]() (de waarde waarvoor de noemer gelijk
(de waarde waarvoor de noemer gelijk ![]() wordt); de horizontale asymptoot is
wordt); de horizontale asymptoot is ![]() (naar welke waarde convergeert de functie voor
(naar welke waarde convergeert de functie voor ![]() of
of ![]() ); het snijpunt met de
); het snijpunt met de ![]() -as bestaat en is
-as bestaat en is ![]() (neem
(neem ![]() ) en het snijpunt met
) en het snijpunt met ![]() -as bestaat niet want de
-as bestaat niet want de ![]() -as (
-as (![]() ) is een asymptoot.
) is een asymptoot.
De grafiek van deze functie laat zich nu snel schetsen:
Voorbeeld 3
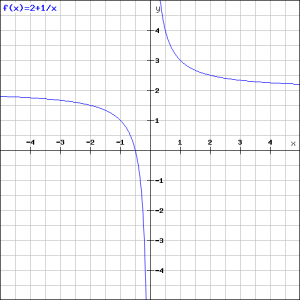
Bepaal van de functie:
![]()
de verticale asymptoot;
de horizontale asymptoot;
het snijpunt met de ![]() -as als dat bestaat;
-as als dat bestaat;
het snijpunt met de ![]() -as als dat bestaat.
-as als dat bestaat.
Schets met behulp van deze resultaten de grafiek.
Wanneer we de asymptoten van ![]() kennen, weten we ook die van de functie
kennen, weten we ook die van de functie ![]() .
.
We zien dat de verticale asymptoot is ![]() (de
(de ![]() -as); de horizontale asymptoot is
-as); de horizontale asymptoot is ![]() (de waarde die
(de waarde die ![]() zal aannemen wanneer
zal aannemen wanneer ![]() of
of ![]() ); het snijpunt met de
); het snijpunt met de ![]() -as bestaat niet (want de
-as bestaat niet (want de ![]() -as is een asymptoot); het snijpunt met de
-as is een asymptoot); het snijpunt met de ![]() -as kan worden berekend uit de vergelijking (neem
-as kan worden berekend uit de vergelijking (neem ![]() ):
):
![]()
![]()
De grafiek laat zich nu gemakkelijk schetsen:
Voorbeeld 4
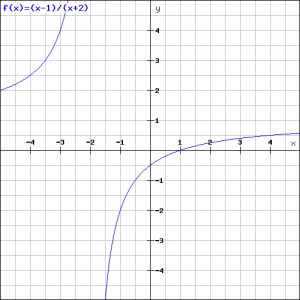
Bepaal van de functie:
![]()
de verticale asymptoot;
de horizontale asymptoot;
het snijpunt met de ![]() -as als dat bestaat;
-as als dat bestaat;
het snijpunt met de ![]() -as als dat bestaat.
-as als dat bestaat.
Schets met behulp van deze resultaten de grafiek.
De functie heeft niet de standaardvorm waarmee we hierboven hebben gewerkt. Maar het is niet moeilijk toch weer die standaardvorm tevoorschijn te toveren.
We kunnen de functie ook anders schrijven:
![]()
Van deze functie weten we dat de verticale asymptoot ![]() is, dat de horizontale asymptoot
is, dat de horizontale asymptoot ![]() is (immers, het tweede lid heeft als asymptoot
is (immers, het tweede lid heeft als asymptoot ![]() ), dat het snijpunt met de
), dat het snijpunt met de ![]() -as is:
-as is: ![]() en dat het snijpunt met de
en dat het snijpunt met de ![]() -as is
-as is ![]() .
.
De grafiek is dan snel gevonden: