Samenvatting en voorbeelden
Om te beginnen een aantal belangrijke rekenregels voor exponenten. Deze komen voortdurend voor en daarom moet je ze goed uit je hoofd kennen.
Rekenen met exponenten
![]()
Voorbeeld: ![]() (dus niet
(dus niet ![]() )
)
![]()
Voorbeeld: ![]()
![]()
Voorbeeld: ![]()
![]()
Voorbeeld: ![]()
![]()
Voorbeeld: ![]()
![]()
![]()
![]()
![]()
Voorbeeld: ![]()
Wortels
Er valt veel meer over wortels te zeggen, maar de volgende eigenschappen moet je in elk geval kennen.
![]() omdat
omdat ![]()
![]() omdat
omdat ![]()
![]() bestaat niet, er is geen reëel getal waarvan het kwadraat
bestaat niet, er is geen reëel getal waarvan het kwadraat ![]() is.
is.
![]() omdat
omdat ![]()
![]() omdat
omdat ![]()
![]() bestaat niet omdat er geen reëel getal is dat een negatief getal als even macht (
bestaat niet omdat er geen reëel getal is dat een negatief getal als even macht (![]() ) heeft (dit geldt overigens voor alle even machtswortels).
) heeft (dit geldt overigens voor alle even machtswortels).
Breuken
Optellen en aftrekken
We beginnen bij breuken met alleen getallen. Breuken kunnen alleen worden opgeteld of afgetrokken wanneer de noemers van de breuken gelijk zijn.
N.B. Een noemer staat onder de deelstreep; is het geen noemer dan is het een teller.
![]()
We hebben gelijke noemers gekregen door de eerste noemer met 3 en de tweede met 7 te vermenigvuldigen (je zou ook kunnen zeggen: door de noemers met elkaar te vermenigvuldigen). Dat mag natuurlijk niet zo maar, de tellers moeten dan ook met 3 respectievelijk 7 worden vermenigvuldigd.
In het volgende voorbeeld zou je gelijke noemers kunnen krijgen door 4 en 6 met elkaar te vermenigvuldigen. Beter is om het zogenaamde kleinste gemeenschappelijke veelvoud van 4 en 6 te vinden en dat is natuurlijk 12.
![]()
Meestal hebben we te maken met breuken met letters. Kijk naar het volgende voorbeeld. We kunnen de noemers gelijk maken door de noemer van de eerste breuk met ![]() en die van de tweede met
en die van de tweede met ![]() te vermenigvuldigen. Natuurlijk geldt ook hier weer: wanneer een noemer/teller met een getal
te vermenigvuldigen. Natuurlijk geldt ook hier weer: wanneer een noemer/teller met een getal ![]() wordt vermenigvuldigd of door een getal wordt gedeeld, dan behoudt de breuk dezelfde waarde wanneer dezelfde bewerking ook op de teller/noemer wordt uitgevoerd. Zie de volgende voorbeelden:
wordt vermenigvuldigd of door een getal wordt gedeeld, dan behoudt de breuk dezelfde waarde wanneer dezelfde bewerking ook op de teller/noemer wordt uitgevoerd. Zie de volgende voorbeelden:
![]()
![]()
![]()
Vermenigvuldigen en delen
Bereken het volgende product van breuken:
![]()
De meeste leerlingen of studenten zullen denken dat dit niet mogelijk is zonder rekenmachine. Maar wanneer de eerder genoemde regel wordt gebruikt, namelijk dat een breuk zijn waarde houdt wanneer teller en noemer door hetzelfde getal ![]() worden gedeeld, is het eenvoudig de berekening uit te voeren.
worden gedeeld, is het eenvoudig de berekening uit te voeren.
Allereerst mogen we de breuk als volgt schrijven:
![]()
Vervolgens delen we teller en noemer door gemeenschappelijke factoren. Als voorbeeld, als we teller en noemer delen door 13, resteert in de teller 1 in plaats van 13 en in de noemer 3 in plaats van 39. Op deze wijze verder gaand krijgen we als resultaat ![]() .
.
We willen vervolgens de volgende breuk vereenvoudigen:
![]()
We weten dat we mogen schrijven (zie hierboven de regels met exponenten):
![]() en
en ![]()
en dus wordt het resultaat:
![]()
Ontbinden in factoren en haakjes wegwerken
Vaak willen we factoren buiten haakjes halen. Dit wordt ook wel ontbinden in factoren genoemd.
(Let op: een onderdeel van een vermenigvuldiging of deling wordt een factor genoemd. Een onderdeel van een optelling of aftrekking wordt een term genoemd.)
![]()
In het linker lid hebben de drie termen de factoren ![]() en
en ![]() gemeen en die 'halen we buiten haakjes'.
gemeen en die 'halen we buiten haakjes'.
Ook omgekeerd komt veel voor. We willen dan zoals dat heet de haakjes wegwerken. De volgende twee formules zijn zeer de moeite waard om te onthouden.
![]()
![]()
Er zijn een paar gevallen die vaak voorkomen en daarom uit het hoofd moeten worden geleerd. Ze staan bekend als merkwaardige producten. Het merkwaardige slaat hierop dat een product van twee tweetermen in het algemeen vier termen oplevert, maar in de volgende gevallen is dat niet zo. Het resultaat kan met bovenstaande formules worden geverifieerd.
![]()
![]()
![]()
Lineaire functies en vergelijkingen
Een lineaire functie (ook wel eerstegraads functie genoemd) heeft de volgende gedaante:
![]()
De grafiek van deze functie is een rechte lijn.
De parameters ![]() en
en ![]() hebben een bijzondere betekenis.
hebben een bijzondere betekenis.
De parameters ![]() is de helling (ook wel richtingscoëfficiënt genoemd) van de lijn. Wanneer
is de helling (ook wel richtingscoëfficiënt genoemd) van de lijn. Wanneer ![]() dan is de lijn stijgend (van links onder naar rechts boven), in het geval
dan is de lijn stijgend (van links onder naar rechts boven), in het geval ![]() is de lijn dalend (van links boven naar rechts onder), wanneer geldt
is de lijn dalend (van links boven naar rechts onder), wanneer geldt ![]() hebben we te maken met een horizontale lijn.
hebben we te maken met een horizontale lijn.
De parameter ![]() geeft aan waar de lijn de
geeft aan waar de lijn de ![]() -as snijdt, namelijk in het punt
-as snijdt, namelijk in het punt ![]() ; alle punten op de
; alle punten op de ![]() -as hebben immers als
-as hebben immers als ![]() -coördinaat
-coördinaat ![]() .
.
Wanneer we het punt willen vinden waar de lijn de ![]() -as snijdt, moeten we
-as snijdt, moeten we ![]() kiezen. Immers, alle punten op de
kiezen. Immers, alle punten op de ![]() -as hebben een
-as hebben een ![]() -coördinaat
-coördinaat ![]() .
.
![]() ,
, ![]() , dus
, dus ![]()
In een lineaire vergelijking heeft de grootste exponent van de variabele ![]() de waarde 1.
de waarde 1.
Los de volgende lineaire vergelijking op, dat wil zeggen, vind de waarde van ![]() waarvoor het linker en rechter lid gelijk zijn.
waarvoor het linker en rechter lid gelijk zijn.
![]()
Kies in deze gevallen de volgend aanpak.
stap 1: verwijder links en rechts de haakjes;
stap 2: neem links en rechts de ![]() -termen samen; doe hetzelfde met de getallen;
-termen samen; doe hetzelfde met de getallen;
stap 3: plaats de ![]() -variabele in het linker lid en het getal in het rechter lid;
-variabele in het linker lid en het getal in het rechter lid;
stap 4: zorg dat het resultaat er als volgt uitziet: ![]() .
.
Voorbeeld 1
stap 1: ![]()
stap 2: ![]()
stap 3: ![]()
stap 4: ![]()
Voorbeeld 2
Soms is een eerstegraads vergelijking vermomd als een hogeregraads vergelijking.
Kijk naar het volgende voorbeeld:
![]()
Bij het vereenvoudigen vallen de derde macht en het kwadraat weg en blijft een eerstegraads vergelijking over:
![]()
![]()
![]()
Lineaire ongelijkheden
Het is belangrijk te onthouden dat het ongelijkheidsteken van een ongelijkheid omdraait als linker en rechter lid met (hetzelfde) negatieve getal worden vermenigvuldigd of door (hetzelfde) negatieve getal worden gedeeld.
Voorbeeld 3
![]()
![]()
![]()
Voorbeeld 4
![]()
Deze ongelijkheid kan worden herschreven als:
![]()
Vermenigvuldig linker en rechter lid met -1 en het ongelijkheidsteken wordt ![]() in plaats van
in plaats van ![]() , dus:
, dus:
![]()
Kwadratische of tweedegraads vergelijkingen
Algemene formule: ![]() , (
, (![]() , immers als
, immers als ![]() is de functie niet kwadratisch).
is de functie niet kwadratisch).
De grafiek is een parabool; ![]() :
: ![]() (dalparabool);
(dalparabool); ![]() :
: ![]() (bergparabool).
(bergparabool).
Het getal ![]() bepaalt het snijpunt van de parabool met de
bepaalt het snijpunt van de parabool met de ![]() -as. Immers, alle punten op de
-as. Immers, alle punten op de ![]() -as hebben de coördinaat
-as hebben de coördinaat ![]() en dus is
en dus is ![]() het snijpunt van de grafiek met de
het snijpunt van de grafiek met de ![]() -as.
-as.
Om snijpunten met de ![]() -as (i.e.,
-as (i.e., ![]() ) te vinden moet je de vergelijking oplossen:
) te vinden moet je de vergelijking oplossen: ![]() .
.
Deze vergelijking heeft overigens niet altijd (reële) oplossingen. Een dalparabool met een minimum boven de ![]() -as en een bergparabool met een maximum onder de
-as en een bergparabool met een maximum onder de ![]() -as hebben geen snijpunt(en) met de
-as hebben geen snijpunt(en) met de ![]() -as. Of een parabool de
-as. Of een parabool de ![]() -as snijdt, hangt af van de discriminant
-as snijdt, hangt af van de discriminant ![]() , zie hieronder.
, zie hieronder.
Hoe lossen we een kwadratische vergelijking ![]() op?
op?
We onderscheiden de volgende methoden:
- Ontbinden in factoren (soms is dat eenvoudig te doen en dan heeft deze methode de voorkeur, maar lang niet altijd is dat het geval);
- De abc-formule (levert altijd een oplossing als die bestaat);
- Bijzondere gevallen.
De abc-formule levert zeker een oplossing als die bestaat, maar de andere methoden zijn soms sneller te berekenen.
Ontbinden in factoren
Probeer de expressie ![]() te schrijven in de vorm
te schrijven in de vorm ![]() . waarin
. waarin ![]() en
en ![]() gehele getallen zijn die
gehele getallen zijn die ![]() als product en
als product en ![]() als som hebben (de zogenaamde som-product methode).
als som hebben (de zogenaamde som-product methode).
Voorbeeld 5
![]() kan worden geschreven als
kan worden geschreven als ![]() want
want ![]() en
en ![]()
![]() kan worden geschreven als
kan worden geschreven als ![]() want
want ![]() en
en ![]()
Deze methode is alleen eenvoudig te gebruiken als ![]() . Indien
. Indien ![]() kunnen linker en rechter lid door
kunnen linker en rechter lid door ![]() worden gedeeld. Echter, wanneer een van de coëfficiënten hierdoor een breuk wordt, is de som-product methode niet te gebruiken.
worden gedeeld. Echter, wanneer een van de coëfficiënten hierdoor een breuk wordt, is de som-product methode niet te gebruiken.
abc-formule
De oplossing van de kwadratische vergelijking ![]() kan worden gevonden door de volgende formule te gebruiken:
kan worden gevonden door de volgende formule te gebruiken:
![]()
Deze formule staat bekend als de abc-formule. D is de discriminant: ![]() .
.
Er zijn drie mogelijkheden:
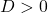 : 2 verschillende oplossingen
: 2 verschillende oplossingen 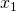 of
of 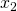
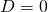 : 1 oplossing (eigenlijk 2 gelijke oplossingen
: 1 oplossing (eigenlijk 2 gelijke oplossingen 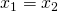 )
)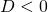 : geen (reële) oplossingen
: geen (reële) oplossingen
Voorbeeld 6
![]()
dus:
![]()
Dus de oplossingen zijn: ![]() of
of ![]() .
.
Deze vergelijking kan ook worden opgelost met de som-product methode. Probeer!
![]()
dus
![]()
Dus de oplossingen zijn ![]() of
of ![]()
Bijzondere gevallen
Het eerste geval is wanneer ![]() .
.
![]() , dus
, dus ![]() , en dus
, en dus ![]() of
of ![]() (vergeet de min-oplossing niet!)
(vergeet de min-oplossing niet!)
In het andere geval geldt ![]() .
.
Dan halen we gewoon de ![]() buiten haakjes.
buiten haakjes.
![]() , dus
, dus ![]() en dus
en dus ![]() of
of ![]() .
.

